「計算はできるけど、文章題ができない！」の、なーぜ？なーぜ??

算数や数学の文章題ができない!!　なぜ？

計算は、できるんです。例えば、中学生の二次方程式。計算問題はできるけど、文章題となれば、手も足も出ない・・・中学生に限らず、小学生、高校生も同じです。それは一体どんな力を身につければいいのでしょうか。

この記事を読んでわかること

毎年どの学年でも指導実績あり！

算数や数学の文章題ができない。これは、算数や数学の力が劣っているということを意味しているわけではありません。だって、これまでみてきた多くの生徒は、計算問題はできるんです。でも、文章題になった途端、何もできない。この状況を、家庭教師として、塾講師として改善に導いた実績があります。闇雲に算数や数学の練習問題をさせることだけではないのです。そのような状況にはちゃんとした理由があり、その対策があることを生徒の成長とともに見てきました。

ゆっくりでもいいので、(数学の文章題の話題ですが)国語に対する正しい認識とその勉強法について、最後まで読んでください。

具体と抽象を理解しよう

結論から言えば、算数や数学の文章問題に書かれている事象は、具体。それを数式という一般(抽象)に置き換えなさい。これが文章問題の本質です。つまり、具体を抽象に変換する力、抽象化する力が問われているのです。

ちょっと難しいですね・・・

具体と抽象の話からやっていきましょう。

小さな子どもが「お母さん、リンゴとバナナが食べたい」と言うと、お母さんは「くだもの売り場に行こうね」と手を引いていく。これ、

リンゴとバナナ：具体
くだもの：抽象

という関係があります。

日常生活で、こういう頭の使い方は自然とやっているのです。

例えば、算数の文章題
「太郎くんは午前9時に家を出て、分速100mで学校に向かい、20分後に到着しました。花子さんは、同じ時刻に家を出て、分速20mで寄り道をせずに学校に向かいました。花子さんは何時何分に学校に到着するでしょうか」
というような問題は、具体的な事象ですよね？

これを、xなどの未知数を文字でおいて式で表す。
数式は、誰がどう見てもそうとしか読み取れない一般的で普遍的、抽象的なものです。
この具体を抽象に置き換える力が弱い場合、文章題が苦手だ、となるのです。

算数セットの「数え棒」の意味

具体と抽象の観点から言えば、数え棒は次のようにみることができる、というお話をします。

小学生の頃、例えばこんな文章題がありました。

「リンゴ１つとミカン１つがあります。合わせていくつですか」。

少し勉強を先取りして、足し算の技術を知っている子どもは「合わせて」と聞けば「足し算だ！」と反射的に目の前にある数字「１」と「１」を足してしまいますが、そんなことをまだ知らない最初の最初は、「リンゴの１」と「ミカンの１」は同じように足してもいいのか？と不安に思ったはずです(幼少すぎて記憶にない人がほとんどだと思いますが)

「リンゴの１」と「ミカンの１」は、具体です。これは、紛れもなく、目の前にある赤いリンゴ１つ、黄色いミカン１つです。この全く違うくだものを、同じものと見做して足すことに違和感を持つのが、幼少の子どもです。具体と具体の全く異なる物体なのですから。そして、「看做す」のは抽象です。この「異なる１」を「同じ」と看做すためには、抽象化の過程を頭の中で経る必要があります。

・ミカンの属性をすべて書き出す

・リンゴの属性をすべて書き出す

そして「数」との観点で共通するものが「１」なのです。

小学１年生にこのことがわかるようにするために、算数セットに数え棒が入っています。

リンゴ１個という具体と、ミカン１個という具体を、「半具体物」である同じ数え棒に置き換える。
そこで、同じとわかったなら、足せるのです。

つまり、

「リンゴ１つとミカン１つがあります。合わせていくつですか」：具体

1+1=2：抽象

小学１年生の足し算の文章題から、このような具体から抽象の変換は行われています。これを計算の技術だけで押し切ってしまうと、抽象化するという頭の使い方が意識されず、もっと複雑な文章題になれば、計算の技術の何を使えばいいのかさえわからず、式が立てられない(抽象化できない)ことになってしまうのです。

それって、国語力！

この「具体から抽象」または、具体と抽象の往還(行ったり来たりしながら考えること)は、国語で鍛えることができます。もちろん算数/数学固有の知識・技能がいらないわけではありませんが、これは「ものの見方」なので、日本語である国語で学ぶことが有効な手立てだと考えています。

日本語で言うと、具体と抽象とは、このような関係にあります。私たちは、日常生活において、具体と抽象という見方で、考えたことを整理しているのです。

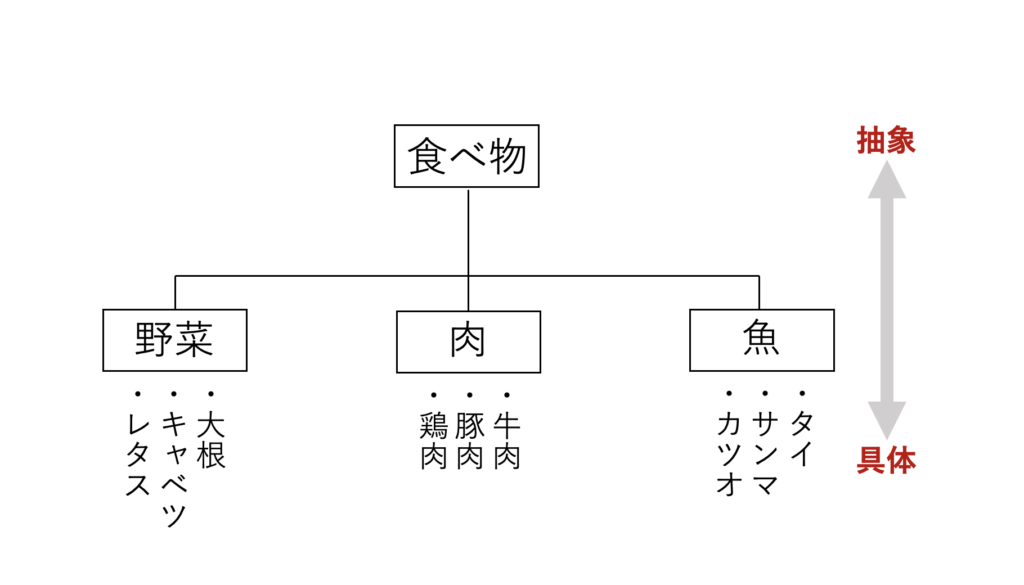
これを長文読解に当てはめると、次のようになります。

＊論説文では

筆者の主張(抽象)＝具体例(具体)

＊小説問題では

登場人物の心情(抽象)＝動作、セリフ、情景描写

という関係に現れます。

明晰な頭脳で学習しよう

このように具体と抽象を意識できる人の頭の中は、いつもスッキリと明晰な状態だと言えます。混沌としていない。だから、算数や数学の文章題の内容が整理できて、抽象化できるのです。

これは「見方」ですから、国語で鍛えた抽象的思考は、当然、文章(数学の文章題)を数式にする抽象化にも対応できることになります。

まずは、日本語で「見方」を練習しよう

というわけで、「計算はできるけど、文章題できない！　を解決！」をお話してきました。

文章題という「具体」を、数式という「抽象」に置き換える訓練は、ぜひ私たちが日頃から使っている日本語でその「見方」を練習してください。

そのことが、算数や数学の文章題を得意にすることにつながります。

このような「見方」が定着するおすすめの問題集を下に推薦いたします。ぜひご購入して、やってみてください。